exercise 5.5

ZIP with MATLAB scripts and note:

exercise 5.5 notes:

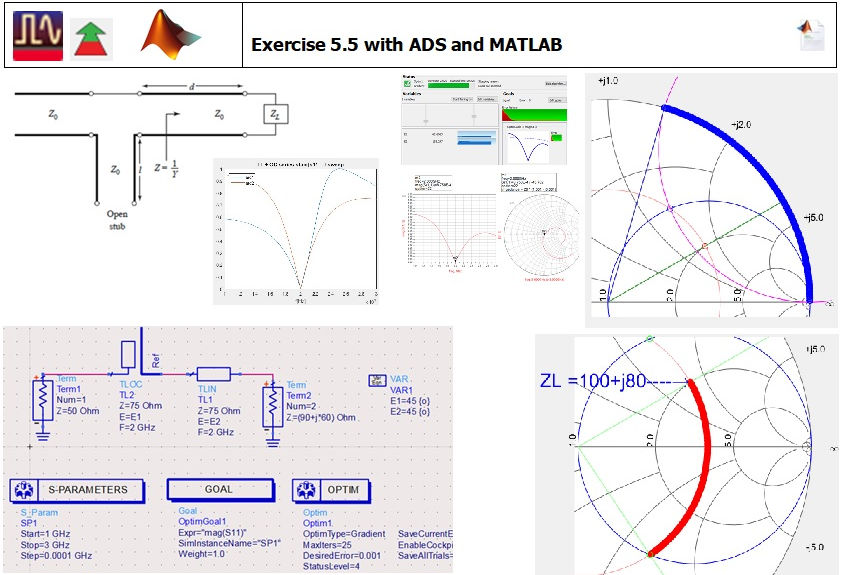
Solving exercise 5.5 with the ADS Optimizer

Single series open circuit stub match

E1(º) is l, D OC stub, D2: open circuit series stub electric length.

E2(º) is d, D Transmission Line, D1: series transmission line electric length.

Comment:

On the right hand side, ADS optimiser apparently accepts variable var_name into the optimiser by simply adding var_name {o}, but the optimiser doesn't start until keying in 'var_name unit opt{a unit to b unit}' where b>a, having previously changed Variable Eq entry mode to Name=Value.

Single series open circuit stub ZL=90+1j*60;Z0=75

Starting optimizer with E1=E2=45º resulting: E1=62.6º E2=155.24º 22 iterations

E = [ 62.6 155.24];D=E/360

D1 = 0.173888888888889 0.431222222222222

Starting optimizer with E1=E2=12º

Result: E1=297.27º E2=260.86º after 15 iterations

E1=297.27º E2=260.86º

E = [297.27 260.86];D=E/360

D = 0.825750000000000 0.724611111111111

Starting optimizer with E1=E2=90º

Result: E1=117.29º E2=80.86º after only 2 iterations

E1=117.29º E2=80.86º

E = [117.29 80.86];D=E/360

D = 0.325805555555556 0.224611111111111

where D is lambda wavelength fraction.

exercise 5.5 with MATLAB

reusing code from 5.3, the lines below

gamma_ZL_angle=angle(gamma_ZL);gamma_ZL_mod=abs(gamma_ZL)

if gamma_ZL_angle<0 gamma_ZL_angle=2*pi+gamma_ZL_angle; end

if gamma_ZL_angle>(2*pi) gamma_ZL_angle=gamma_ZL_angle-2*pi; end

Smith_plotZ(ax(1),ZL,Z0,[1 0 0])

replaced with just the line below.

The 4 lines on left hand side now in function Smith_plotZ

[gamma_ZL_angle,gamma_ZL_mod]=Smith_plotZ(ax(1),ZL,Z0,[1 0 0],1)

Calculating D1_TL

Z0=75; ZL=90+1j*60;

gamma_ZL=(ZL-Z0)/(ZL+Z0);

hf(1)=figure(1);sm(1)=smithchart;ax(1)=hf(1).CurrentAxes;hold(ax(1),'on')

Smith_plotZ(ax(1),ZL,Z0,[1 0 0],1)

Smith_plotRefLine2PhaseCircle(ax(1),ZL,Z0,[.6 1 .6])

[x_swr,y_swr]=Smith_plotGammaCircle(ax(1),ZL,Z0,[1 .6 .6])

[xr1,yr1]=Smith_plotRcircle(ax(1),Z0,Z0,[0 0 1])

[xint,yint]=intersections(x_swr,y_swr,xr1,yr1,1);

plot(ax(1),xint,yint,'go')

refl_zx1=xint(1)+1j*yint(1);

refl_zx1_angle=angle(refl_zx1);refl_zx1_mod=abs(refl_zx1)

if refl_zx1_angle<0 refl_refl_zx1_angle=2*pi+refl_zx1_angle; end

if refl_zx1_angle>(2*pi) refl_zx1_angle=refl_zx1_angle-2*pi; end

% check

Z_1=Z0*(1+refl_zx1)/(1-refl_zx1)

real(Z_1)

Smith_plotRefLine2PhaseCircle(ax(1),Z_1,Z0,[.6 1 .6])

da=1/100;arc1=da

a0=gamma_ZL_angle;a1=refl_zx1_angle;gamma_mod=gamma_ZL_mod

a0*180/pi

a1*180/pi

if a0<0 a0=2*pi+a0; end % avoid start with any negative angle

if a0>(2*pi) a0=a0-2*pi; end

if a1<1 a1=2*pi+a1; end

if a1>(2*pi) a1=a1-2*pi; end

% preventing while loop missing target because step not small enough

a0=da*floor(1/da*a0)

a1=da*floor(1/da*a1)

while da*floor(1/da*abs(a0-a1))>da

a0=a0-da;arc1=arc1+da;

if a0<0 a0=2*pi+a0; end % avoid negative angles

if a0>(2*pi) a0=a0-2*pi; end

gamma=gamma_mod*(cos(a0)+1j*sin(a0));

plot(ax(1),real(gamma),imag(gamma),'ro','LineWidth',1.5);

% drawnow

end

plot(ax(1),xint,yint,'go')

% checking stub input impedance already on r=1 circle

Z_1

isequal(da*floor(1/da*real(Z_1)),…

da*floor(1/da*real(Z0)))

D1_TL_lambda=arc1/(4*pi)

D1_TL_angle_deg=D1_TL_lambda*180/.5

lambda/2 is 180º electric length that in turn is 360º on Smith Chart

..

Calculating D2_TL

hf(2)=figure(2);sm(2)=smithchart; ax(2)=hf(2).CurrentAxes; hold(ax(2),'on')

gamma_ZL=Smith_plotZ(ax(2),ZL,Z0,[1 0 0],0)

Smith_plotRefLine2PhaseCircle(ax(2),ZL,Z0,[.6 1 .6])

[x_swr,y_swr]=Smith_plotGammaCircle(ax(2),ZL,Z0,[1 .6 .6])

[xr1,yr1]=Smith_plotRcircle(ax(2),Z0,Z0,[0 0 1])

plot(ax(2),xint,yint,'go')

refl_zx2=xint(2)+1j*yint(2); % 2nd intersection point

refl_zx2_angle=angle(refl_zx2);refl_zx2_mod=abs(refl_zx2)

if refl_zx2_angle<0 refl_refl_zx2_angle=2*pi+refl_zx2_angle; end

if refl_zx2_angle>(2*pi) refl_zx2_angle=refl_zx2_angle-2*pi; end

% check

Z_2=Z0*(1+refl_zx2)/(1-refl_zx2)

real(Z_2)

Smith_plotRefLine2PhaseCircle(ax(2),Z_2,Z0,[.6 1 .6])

da=1/100;arc2=da

a0=gamma_ZL_angle;a1=refl_zx2_angle;gamma_mod=gamma_ZL_mod

if a0<0 a0=2*pi+a0; end % avoid starting with negative angles

if a0>(2*pi) a0=a0-2*pi; end

if a1<1 a1=2*pi+a1; end

if a1>(2*pi) a1=a1-2*pi; end

a0=da*floor(1/da*a0)

% this prevents while loop spinning endlessly if step not small enough

a1=da*floor(1/da*a1)

while da*floor(1/da*abs(a0-a1))>da

a0=a0-da;arc2=arc2+da;

if a0<0 a0=2*pi+a0; end % avoid negative angles

if a0>(2*pi) a0=a0-2*pi; end

gamma=gamma_mod*(cos(a0)+1j*sin(a0));

plot(ax(2),real(gamma),imag(gamma),'ro','LineWidth',1.5);

% drawnow

end

plot(ax(2),xint,yint,'go')

checking stub input impedance already on r=1 circle

Z_2

isequal(da*floor(1/da*real(Z_2)),…

da*floor(1/da*real(Z0)))

D2_TL_lambda=arc2/(4*pi)

D2_TL_angle_deg=D2_TL_lambda*180/.5

=

75.003511824677943 +56.434078007705629i

=

logical

1

D2_TL_lambda =

0.480647928137517

D2_TL_angle_deg =

1.730332541295062e+02

Calculating stub lenght Dstub1

hf(3)=figure(3);sm(3)=smithchart; ax(3)=hf(3).CurrentAxes; hold(ax(3),'on');

gamma_ZL=Smith_plotZ(ax(3),ZL,Z0,[1 0 0],0)

Smith_plotRefLine2PhaseCircle(ax(3),ZL,Z0,[.2 .6 .2])

[x_swr,y_swr]=Smith_plotGammaCircle(ax(3),ZL,Z0,[1 .6 .6])

[xr1,yr1]=Smith_plotRcircle(ax(3),Z0,Z0,[0 0 1])

plot(ax(3),xint,yint,'go')

% 1st intersection

refl_zb1=xint(1)+1j*yint(1);

refl_zb1_angle=angle(refl_zb1);refl_zb1_mod=abs(refl_zb1)

if refl_zb1_angle<0 refl_zb1_angle=2*pi+refl_zb1_angle; end

if refl_zb1_angle>(2*pi) refl_zb1_angle=refl_zb1_angle-2*pi; end

Zbs=Z0*((1+refl_zb1)/(1-refl_zb1))

refl_zstub=conj(refl_zb1) % where stub imag(Zin) has to be

plot(ax(3),real(refl_zstub),imag(refl_zstub),'bo')

Zbs2=Z0*(1+refl_zstub)/(1-refl_zstub)

Smith_plotBarc(ax(3),Zbs2,Z0,[1 0 1]) % reading stub reactance

Zbs3=1j*imag(Zbs2)

refl_Zstub=(Zbs3-Z0)/(Zbs3+Z0)

plot(ax(3),real(refl_Zstub),imag(refl_Zstub),'ro')

Smith_plotRefLine2PhaseCircle(ax(3),Zbs3,Z0,[.2 .2 .8])

% Z Smith chart -pi: SC 0: OC. Y Smith chart 0: SC -pi: OC

da=1/100;a_stub=[angle(refl_Zstub):-da:0];arc_stub1=da;

for k=1:1:numel(a_stub)

gamma_stub=cos(a_stub)+1j*sin(a_stub);

arc_stub1=arc_stub1+da;

plot(ax(3),real(gamma_stub),imag(gamma_stub),'bo','LineWidth',1.5);

end

arc_stub1=arc_stub1-da;

% from the arc on Smith chart

arc_stub1_lambda=.25/pi*arc_stub1

% same as

Dstub1_lambda=arc_stub1/(4*pi)

Dstub1_angle_deg=arc_stub1/2*360/(2*pi)

Calculating stub lenght Dstub2

hf(4)=figure(4);sm(4)=smithchart; ax(4)=hf(4).CurrentAxes; hold(ax(4),'on');

gamma_ZL=Smith_plotZ(ax(4),ZL,Z0,[1 0 0],0)

Smith_plotRefLine2PhaseCircle(ax(4),ZL,Z0,[.2 .6 .2])

[x_swr,y_swr]=Smith_plotGammaCircle(ax(4),ZL,Z0,[1 .6 .6])

[xr1,yr1]=Smith_plotRcircle(ax(4),Z0,Z0,[0 0 1])

plot(ax(4),xint,yint,'go')

% 2nd intersection

refl_zb2=xint(2)+1j*yint(2);

refl_zb2_angle=angle(refl_zb2);refl_zb2_mod=abs(refl_zb2)

if refl_zb2_angle<0 refl_zb2_angle=2*pi+refl_zb2_angle; end

if refl_zb2_angle>(2*pi) refl_zb2_angle=refl_zb2_angle-2*pi; end

Zbs=Z0*((1+refl_zb2)/(1-refl_zb2))

refl_zstub=conj(refl_zb2) % where stub imag(Zin) has to be

plot(ax(4),real(refl_zstub),imag(refl_zstub),'bo')

Zbs2=Z0*(1+refl_zstub)/(1-refl_zstub)

Smith_plotBarc(ax(4),Zbs2,Z0,[1 0 1]) % reading sought stub reactance

Zbs3=1j*imag(Zbs2)

refl_Zstub=(Zbs3-Z0)/(Zbs3+Z0)

plot(ax(4),real(refl_Zstub),imag(refl_Zstub),'ro')

Smith_plotRefLine2PhaseCircle(ax(4),Zbs3,Z0,[.2 .2 .8])

angle_refl_Zstub=angle(refl_Zstub) % avoid negative angles

if angle_refl_Zstub<0 angle_refl_Zstub=2*pi+angle_refl_Zstub; end

if angle_refl_Zstub>(2*pi) angle_refl_Zstub=angle_refl_Zstub-2*pi; end

% Z Smith chart -pi: SC 0: OC, Y Smith chart 0: SC -pi: OC

da=1/100;a_stub=[angle_refl_Zstub:-da:0];arc_stub1=da;

for k=1:1:numel(a_stub)

gamma_stub=cos(a_stub)+1j*sin(a_stub);

arc_stub1=arc_stub1+da;

plot(ax(4),real(gamma_stub),imag(gamma_stub),'bo','LineWidth',1.5);

end

arc_stub1=arc_stub1-da;

% from the arc on Smith chart

arc_stub1_lambda=.25/pi*arc_stub1

% same as

Dstub1_lambda=arc_stub1/(4*pi)

Dstub1_angle_deg=arc_stub1/2*360/(2*pi)

arc_stub1_lambda = 0.148014097075463

Dstub1_lambda = 0.148014097075463

Dstub1_angle_deg = 53.285074947166599

arc_stub2_lambda = 0.353323973664004

Dstub2_lambda = 0.353323973664004

Dstub2_angle_deg = 1.271966305190413e+02

Frequency Sweep

Putting transmission line and stub lengths together

D=[D1_TL_lambda D2_TL_lambda;

Dstub2_lambda Dstub1_lambda]

Let be the following f0 and band:

c0=2.998e8;

f0=2e9;

df=1e5;f1=1e9;f2=3e9;f=[f1:df:f2];

Then the physical lengths of all transmission lines and stubs are:

L=D*c0/f0

s11=zeros(size(D,2),numel(f));

ZinTL=zeros(size(D,2),numel(f));

Zin_stb_oc=zeros(size(D,2),numel(f));

Zin=zeros(size(D,2),numel(f));

for k=1:1:size(L,2)

ZinTL(k,:)=Z0*(ZL+1j*Z0*tan(2*pi*f/c0*L(1,k)))./…

(Z0+1j*ZL*tan(2*pi*f/c0*L(1,k))); % series transmission line

end

for k=1:1:size(D,2) % open circuit shunt stub

Zin_stb_oc(k,:)=Z0./(1j*tan(2*pi*L(2,k)*f/c0));

impedance

end

Zin=ZinTL+Zin_stb_oc;

s11=(Zin-Z0)./(Zin+Z0);

s11_mod=abs(s11);

hf(10)=figure(10);

plot(f,s11_mod(1,:));plot(f,s11_mod(2,:));grid on

for k=1:1:size(s11_mod,1)

hf(10)=figure(10);plot(f,s11_mod(k,:));hold all;

end

grid on

title('TL + OC series stub |s11| - f sweep');xlabel('f[Hz]')

legend('arc1','arc2','eq1','eq2','Location','northwest')

D =

0.231397640694349 0.424104164889466

0.148014097075463 0.353323973664004

L =

0.034686506340083 0.063573214316931

0.022187313151612 0.052963263652234

There's also an alternative graph to find the required transmission line and stub lengths; |s11| surface.

clc;clear all;close all

ZL=90+1j*60;Z0=75;

Dstep=.001;drange=[0:Dstep:1];

D1=drange;D2=D1;

[D1,D2]=meshgrid(drange);

Z1=Z0*(ZL+1j*Z0*tan(2*pi*D1))./(Z0+1j*ZL*tan(2*pi*D1));

Zin_stub=Z0./(1j*tan(2*pi*D2)); % series oc stub

Zin=Z1+Zin_stub;

s11=(Zin-Z0)./(Zin+Z0);

surf(abs(s11),'LineStyle','none')

ax=gca

xlabel('D1');ylabel('D2');

ax.XTickLabelMode='manual'; ax.YTickLabelMode='manual';

ax.XTickLabel=[0:0.1:1];ax.YTickLabel=[0:0.1:1];

ax.XTick=[0:100:1000];ax.YTick=[0:100:1000];

ax.PlotBoxAspectRatio=[1 1 1]

hold all;x0=find(drange==.5) % plotting corner to box D1<.5 D2<.5

plot3([x0 x0 0],[0 x0 x0],[5 5 5],'Color',[1 0 0],'LineWidth',3)

% moving camera birdeye view

ax.CameraPosition=[500 500 10]

camzoom(ax,1.5) % zoom in a bit, camzoom is cumulative

% zoom_factor within [0 1) zooms out zoom_factor>1 zooms in

ax.CameraUpVector = [0 1 0]; % camera attitude

ax.CameraTarget = [500 500 0]; % centring

ax.CameraViewAngle =8*pi; % focus

automating peaks capture: findpeaks with MinPeakProminence=2.5 returns the right amount of peaks. MinPeakProminence larger or smaller than 2.5 then either too few or too many peaks.

With MinPeakHeight=2 command findpeaks doesn't catch the right amount of peaks for any MinPeakDistance, going from 6 peaks only to too many peaks.

With Threshold=2 doesn't catch a single peak but Threshold=1 gets the right amount of peaks.

To get zeros exact locations, it's useful to invert |s11| surface just plotted, with the Laplacian of the surface, command del2

V=1e3*del2(abs(s11));

figure(2);ax=gca;surf(V,'Lines','none');

xlabel('D1');ylabel('D2');

ax.XTickLabelMode='manual';

ax.YTickLabelMode='manual';

ax.XTickLabel=[0:0.1:1];ax.YTickLabel=[0:0.1:1];

ax.XTick=[0:100:1000];ax.YTick=[0:100:1000];

[pks,locs]=findpeaks(V( : ),'Threshold',1);

[nd1,nd2]=ind2sub(size(V),locs);

hold all;figure(2);plot3(nd2,nd1,V(nd2,nd1)+2,'ro'); % plot peaks

ax.PlotBoxAspectRatio=[1 1 1]

x0=find(drange==.5) % plot corner to box D1<.5 D2<.5

figure(2);

plot3([x0 x0 0],[0 x0 x0],[.5 .5 .5],'Color',[1 0 0],'LineWidth',3)

ax2=gca

ax2.CameraPosition=[500 500 10] % moving camera birdeye view

ax2.CameraUpVector = [0 1 0]; % camera attitude

camzoom(ax,1.5) % zoom in a bit, camzoom is cumulative

% zoom_factor within [0 1) zooms out zoom_factor>1 zooms in

ax2.CameraTarget = [500 500 0]; % centring

abs(s11(sub2ind(size(V),nd1,nd2)))

unique(sort(drange(nd1)))

numel(nd1)

among these stub lengths

D1=unique(drange(nd1))

D2=unique(drange(nd2))

the stub lengths inside D<.5 are the smallest ones

Dstub1= D1([1 2])

Dstub2= D2([1 2])

= 0.001390798787950

0.001390798787950

0.002883920448033

0.001390798787950

0.002883920448033

= 0.1470 0.3530 0.6470 0.8530

= 8

= 0.1470 0.3530 0.6470 0.8530

= 0.1740 0.4820 0.6740 0.9820

Dstub1 = 0.1470 0.3530

Dstub2 = 0.1740 0.4820

D1= D1([1 2]) % series transmission line

D2= D2([2 1]) % series oc stub

s11=zeros(1,numel(f));s11_mod=zeros(1,numel(f));

L1=D1*c0/f0

L2=D2*c0/f0

ZinTL=Z0*(ZL+1j*Z0*tan(2*pi*L2(1) *f/c0))./(Z0+1j*ZL*tan(2*pi*L2(1) *f/c0));

Zin_stb_oc=Z0./(1j*tan(2*pi*L1(1)*f/c0)); % open stub

Zin=ZinTL+Zin_stb_oc;

s11_mod=abs((Zin-Z0)./(Zin+Z0));

figure(2);plot(f,s11_mod);grid on

hold all

ZinTL=Z0*(ZL+1j*Z0*tan(2*pi*L2(2) *f/c0))./(Z0+1j*ZL*tan(2*pi*L2(2) *f/c0));

Zin_stb_oc=Z0./(1j*tan(2*pi*L1(2)*f/c0)); % open stub

Zin=ZinTL+Zin_stb_oc;

s11_mod=abs((Zin-Z0)./(Zin+Z0));

figure(2);plot(f,s11_mod);grid on

quick check how short circuit and open circuit stubs behave over frequency:

Zin_sc_stub=1j*Z0*tan(beta*L)

Zin_oc_stub=-1j*Z0*cot(beta*L)

quick check how short circuit and open circuit stubs behave over frequency:

Zin_sc_stub=1j*Z0*tan(beta*L)

Zin_oc_stub=-1j*Z0*cot(beta*L)

da=pi/2000;a=[-2*pi:da:2*pi];

y_OC=-cot(a); y_SC=tan(a);

figure;plot(a,y_OC,a,y_SC);

grid on;axis([-2*pi 2*pi -10 10])

legend('SC','OC')

ylabel('Stub Z_i_n');xlabel('\betaL')

xticks([-2*pi -2*pi*3/4 -pi -pi/2 0 pi/2 pi 3*pi/2 2*pi])

xticklabels({'-2\pi','-3\pi/4','-\pi','-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi'})