exercise 6.4

c0=2.998792586

er=1

f1=4.9e9;f2=5.1e9;f0=5e9

Nf=1e6                         % amount frequency points between f1 f2

df=abs(f1-f2)/(Nf+1)          % frequency resolution

f=[f1:df:f2];

delta_f=f-f0;

       

lambda1=c0/f1;lambda2=c0/f2;lambda0=c0/f0

dlambda=abs(lambda1-lambda2)/(Nf+1) 

lambda=[lambda2:dlambda:lambda1];

      

L=lambda0/2

       

RLoad=0;Rgen=50;

ZL=RLoad;               % load assumed constant resistance over all band

Z0=Rgen;                                           

      

beta=2*pi./lambda;

       

N=1e4

dL=L/N

D_right=[1:1:floor((N)/2)]/N;

D_left=.5-D_right;

% same as

% D_left=D_right([end:-1:1]);

 

Zin_right=1j*Z0*tan(2*pi/lambda0*D_right*lambda0);  

Zin_left=1j*Z0*tan(2*pi/lambda0*D_left*lambda0);  

% same as

% Zin_left=1j*Z0*tan(2*pi/lambda0*(1-D_right)*lambda0);  

 

figure(1);

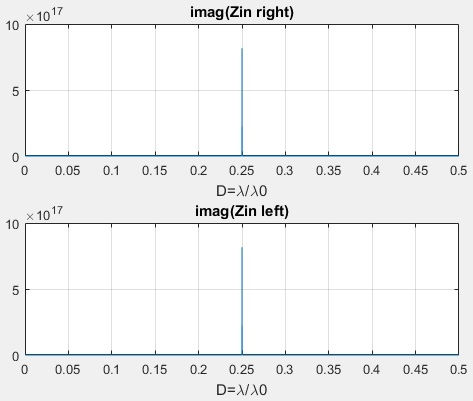
subplot(2,1,1);plot(D_right,imag(Zin_right));

grid on;title('imag(Zin right)');xlabel('D=\lambda/\lambda0')

subplot(2,1,2);plot(D_right,imag(Zin_left));

grid on;title('imag(Zin left)');xlabel('D=\lambda/\lambda0')

 

% it looks like as if ZRiight=ZLeft instead of the expected

 

ZRight=conj(ZLeft).

% The narrow spikes in previous graph hide the tagent is anti-symmetric

       

 

 

nnz(Zin_right==conj(Zin_left))

 

numel(Zin_right)